时序逻辑电路的特点

时序逻辑电路的特点

    在第三章所讨论的组合逻辑电路中，任一时刻的输出信号仅仅取决于该时刻的输入信号，而与电路原来的输出状态无关，这也是组合逻辑电路在逻辑功能上的共同特点。本章将要介绍另一种类型的逻辑电路，其功能特点是任一时刻的输出信号不仅取决于当时的输入信号，而且还取决于电路原来的状态，也即与以前的输入有关，具有这种功能特点的电路叫做时序逻辑电路。
    时序逻辑电路简称时序电路，其结构特点是由存储电路和组合电路两部分组成，或通俗地说由触发器和门电路组成，如图5.1.1所示。时序电路的状态是由存储电路来记忆的，因而在时序逻辑电路中，触发器是必不可少的，而组合逻辑电路在有些时序电路中则可以没有。

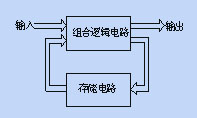
图5.1.1 时序逻辑电路的结构框图

    根据电路状态转换情况的不同，时序电路又分为同步时序逻辑电路和异步时序逻辑电路两大类。在同步时序电路中，所有触发器的时钟输入端CP都连在一起，在外加的时钟脉冲CP作用下，凡是具备翻转条件的触发器在同一时刻改变状态。也就是说，触发器的状态更新与外加时钟脉冲CP的有效触发沿是同步的。而在异步时序逻辑电路中，外加时钟脉冲CP只触发部分触发器，其余触发器则是由电路内部信号触发的，因此，凡具备翻转条件的触发器状态的翻转有先有后，并不都和时钟脉冲CP的有效触发沿相同步。

时序逻辑电路的分析方法

    分析一个时序电路，就是要找出给定时序电路的逻辑功能。具体地说，就是要求找出电路的状态和输出状态（一般指进位输出、借位输出等）在输入变量和时钟信号作用下的变化规律。

在同步时序逻辑电路中，由于所有触发器都由同一个时钟信号CP来触发，它只控制触发器的翻转时刻，而对触发器翻转到何种状态并无影响。所以在分析同步时序逻辑电路时，可以不考虑时钟条件。

基本分析步骤：

1．  写出方程式

输出方程：时序逻辑电路的输出表达式。

驱动方程(又称激励方程)根据给定的电路，分别写出各触发器输入端的逻辑表达式。如JK触发器J和K输入端的逻辑表达式，D触发器D输入端的逻辑表达式，它通常为各触发器现态及输入变量的函数。

2．  求出状态方程式

将驱动方程代入相应触发器的特性方程，便可求出该触发器的次态方程，时序逻辑电路的状态方程由各触发器的次态方程组成。

3．  列出状态转换真值表

将电路现态的各种取值代入状态方程和输出方程中进行计算，按列求出各触发器的次态和输出，从而列出状态转换真值表。在没有给出现态的起始值时，一般按二进制自然序从小到大列出所有可能的现态，时序逻辑电路的输出状态，由电路的现态来决定。

4．  画出状态转换图和时序图

状态转换图是指电路由各现态转换到相应次态的示意图。它反映了时序逻辑电路状态转换的规律。电路的时序图是在时钟脉冲CP作用下，各触发器状态变化的波形图，它形象地表达了输入信号、输出信号、电路状态等的取值在时间上的对应关系。

5．  逻辑功能说明

根据状态转换图（当然也可根据状态转换表）来说明电路的逻辑功能。

三、 时序逻辑电路的分析实例

[例5.1.1]试分析图5.1.2所示电路的逻辑功能。

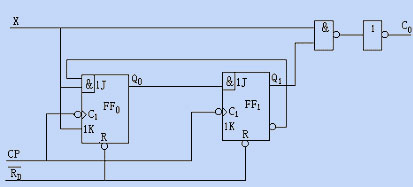
图5.1.2 待分析时序逻辑电路

解：（1）写出方程式

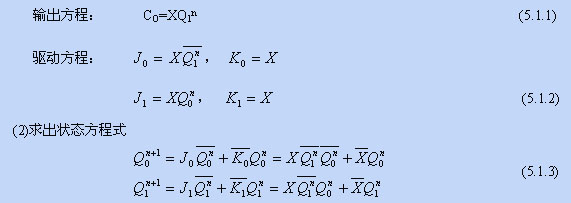
请注意在写状态方程时，变量前后次序一般按输入变量、各触发器现态从高位到低位排列，以便于下一步列写状态转换表。                             

(3)进行状态计算，列出状态转换表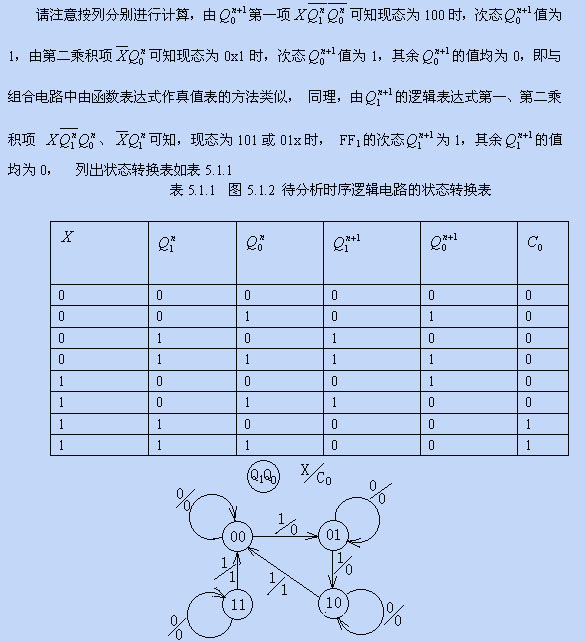  

图5.1.3  状态转换图

（4）画出状态转换图，如图5.1.3所示，其中X、C0用X/C0表示。斜线上方表示输入X的值，下方表示输出C0的值。

状态转换图5.1.3表明，图5.1.2所示电路是一个可控的同步三进制计数器，其中X是控制输入端。当X=0时，计数器停止计数，保持现状态不变；当X=1时，计数器成为三进制递增计数器，计数顺序是    

而“11”状态是无效状态，电路若处于“11”状态，则在CP脉冲作用下可以进入有效状态“00”。因此，图5.1.2计数器可以自启动。

[例5.1.2]试分析图5.1.4所示电路的逻辑功能并画出时序图。

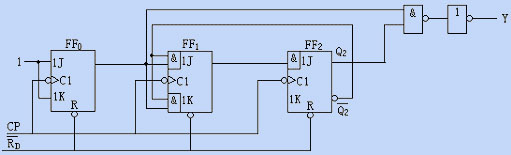
图5.1.4[例5.1.2]待分析时序逻辑电路

解：分析步骤如下：

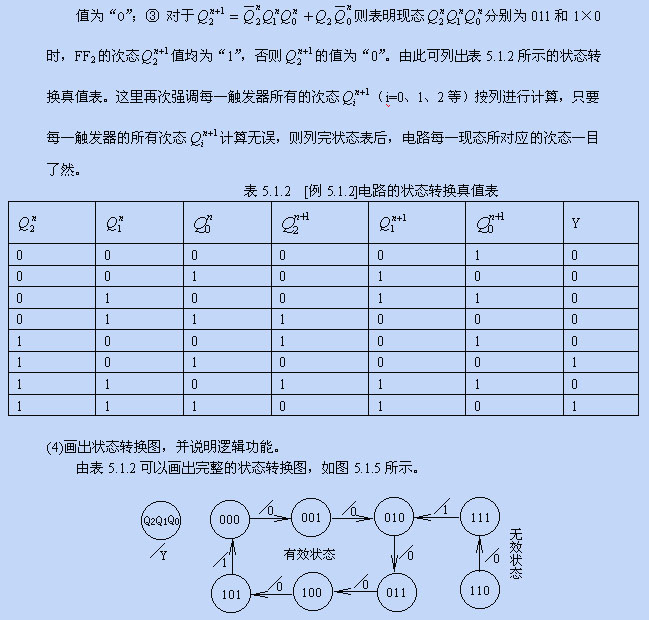
 图5.1.5 [例5.1.2]的状态转换图

可见，其中000、001、010、011、100、101六个状态是有效状态，图5.1.4电路在输入第6个计数脉冲CP后，返回到起始的000状态。同时输出端Y输出一个进位脉冲。而110和111是两个无效状态，若由于干扰或某种原因使电路处于无效状态，最多经过两个CP后能进入有效状态010。因此，图5.1.4所示电路为同步六制递增计数器，具有自启动能力。

（5）画出时序图如图5.1.6所示（据六个有效状态依次画出）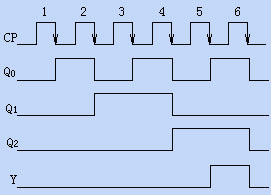

图5.1.6  [例5.1.2]所示电路的时序图